Университет Федосеева
Кое-что о Федосееве Р. Ю.
Портал -Университет Федосеева-
понедельник, 8 ноября 2004 г.
Пока на сайте – http://robfed.narod.ru скоро на сайте – http://fedoseev.info
e-mail: robertfedoseev@nm.ru
ДЕШГРАММНАЯ ПИСЬМЕННОСТЬ ФЕДОСЕЕВА
КОНСПЕКТ ЛЕКЦИЙ-СЕМИНАРОВ
Лекция № 0. (см. на сайте http://dpf2004.narod.ru)
Лекция № 1. (см. на сайте http://dpf2004001.narod.ru )
Лекция № 2. (см. на сайте http://dpf2004002.narod.ru)
Лекция № 3. (версию с рисунками см. на сайте http://dpf2004003.narod.ru)
Лекция № 4. (версию с рисунками см. на сайте http://dpf2004004.narod.ru)
Лекция № 5. (версию с рисунками см. на
сайте http://dpf2004005.narod.ru)
Начнём
семинар с рассмотрения самого главного – с МСКФ – Многомерной Системы Координат
Федосеева.
Напомним
принцип всем известной Ортогональной Декартовой Системы Координат (ОДСК или
просто ДСК – Декартовой Системы Координат).
Рис. 1
Главная задача, которая решается с
помощью ДСК – нахождение точки по заданным координатам. А также обратная
задача, когда дана точка и необходимо найти её координаты.
Рис. 2 и Рис. 3.
Важно иметь
в виду, что ВСЕГДА Система Координат должна быть задана. А именно, надо
перечислить заданные переменные и их обозначения, например,
Переменную № 1 обозначим
буквой «х»,
Переменную № 2 обозначим буквой «у».
Для
изображения свой СК Рене Декарт (ХХII век) взял две
пересекающиеся под прямым углом прямые. Эти прямые называются осями.
Горизонтальная ось называется «осью абсцисс» (или просто абсцисса, она обычно,
но не обязательно, обозначается буквой «х»). Вертикальная ось называется «осью
ординат» (или просто ордината, она обычно, но не обязательно, обозначается
буквой «у»). Этот «крест» является знаком, который предложил Декарт.
В ДСК оси
абсцисс и ординат представляют действительные числа, и, следовательно, в том
числе, целые числа (целые числа являются подмножеством множества действительных
чисел, среди которых, напомню, могут быть не целые, рациональные,
иррациональные).
В центре
(в точке пересечения осей, говорят: «в начале координат») находится число «0».
Нуль был осознан, как число, именно, благодаря ДСК.
На
чертеже оси должны быть нормированы, то есть, должен быть указан масштаб.
Например, число «1» находится на втором конце отрезка прямой, первый из которых
находится в точке «0». При этом отрезок длиной «1» берётся, например, равным
одному сантиметру. Следовательно, точка «2» находится на расстоянии 2 см от
начала координат и т.д. При этом заданные масштабы на разных осях (абсцисс и
ординат) могут быть как одинаковыми, так и разными. Мы договоримся о том, что
эти масштабы будут одинаковыми.
Для
нахождения точки по её координатам последние должны быть также заданы.
Например: х
= 6, у = 3.
Находим точку по этим координатам. Для
этого откладываем от начала координат на оси абсцисс отрезок (координату) х,
равную 6 см, а на оси ординат отрезок (координату) у, равную 3 см. Из концов
этих отрезков восстанавливаем перпендикуляры, то есть линии параллельные
противоположным осям. Из точки х = 6 проводим линию параллельную оси у, а из
точки у = 3 – линию параллельную оси х. На пересечении перпендикуляров находим
искомую точку, соответствующую заданным координатам.
Рис. 4.
Обратная задача, то есть, нахождение
координат по заданной точке в заданной и сконструированной ДСК решается
следующим образом.
Из
заданной точки «опускаются» перпендикуляры на оси абсцисс и ординат, и на
пересечении этих перпендикуляров с соответствующими осями находят концы
отрезков, являющихся координатами заданной точки, если их измерить от начала
координат до этих точек пересечения.
Примечание 1.
Мы намеренно объясняем всё подробно. Это
необходимо для как можно более полного осмысления этих построений и смысла
применения ДСК. Обычно все эти подробности опускаются, что, с нашей точки
зрения, недопустимо в учебном процессе, в школе, вузе и т.п. Особенно, когда
обучение происходит в группе. Кто-то из группы уже догадался или знал раньше, А
другие вообще ничего не понимают. Поэтому, если учитель будет ориентироваться
на «быстрых разумом невтонов», для остальных даже такие простые вещи, как ДСК
останутся «тайной за семью печатями».
Конечно, если все подробно
объяснять, «быстрые» начнут скучать. В
этом – противоречивые условия группового обучения, которые трудно преодолеть.
Одним из способов такого преодоления может быть организация такого общения
между учащимися, при котором «быстрые» обучают «медленных». Радикальным же
решением этой проблемы является организация процесса индивидуального обучения.
Ведь «всякое знание самостоятельно» (Л. Н. Толстой).
Полная же индивидуализация обучения чревата
отрывом учащегося от социума – затруднённая социальная адоптация.
В
какой-то мере это противоречие снимается с помощью организации такого процесса,
когда учащиеся работают в группе (например, в школьном классе), но у каждого из
них есть индивидуальный инструмент (компьютер?), с помощью которого каждый
решает индивидуальные задаче в том темпе, в котором он сможет освоить учебный
материал. Учитель при этом выступает в качестве организатора, координатора,
исследователя и разработчика новых пособий, контролёра и т.д.
Продолжим.
Таким образом, с помощью ДСК мы находим
точки по заданным двум координатам.
А что если задана СК не с двумя
переменными, а с тремя или более?
Переменная х,
переменная у, переменная z и т.д.
Для изображения трёхмерной СК, то есть
заданной Многомерной СК с тремя переменными придуман способ, называемый
изометрией.
Рис. 5.
Однако необходимо заметить, что искомая точка
(если ни одна из трёх координат не равна нулю), хотя она нарисована на плоскости бумаги, на самом
деле находится в неком трёхмерном пространстве, которые мы представляем в нашем
воображении.
Когда же задана система координат,
содержащая белее трёх переменных, до настоящего времени, то есть, до
изобретения МСКФ, никакого удобного и простого изображения этой системы (для
решения задачи о нахождении точки по координатам), по моим сведениям, не
существовало. Если кому-нибудь из слушателей известен такой способ изображения,
я прошу его выйти и показать хотя бы случай для четырёх переменных.
Поскольку, никто ничего не предлагает,
постольку, я продолжаю рассказ о МСКФ.
Замечу только, что решение этой задачи
искали многие. Так, например, Знаменитый математик Минковский хотел помочь в
понимании теории относительности Эйнштейна, пытаясь показать четырёхмерное
пространство-время, используя модернизированную им ДСК. Однако, насколько мне
известно, из этого ничего не вышло. Минковский на этой почве заболел и попал в
психиатрическую больницу. Можно сказать, что после этого мало кто пытался
решить эту задачу, опасаясь последствий, хотя удобство показа МСК на плоскости
(поверхности экрана, на бумаге и т.п.) невозможно переоценить.
Это связано с экзистенцией человека.
Хотелось бы всё увидеть в наиболее простом и удобном для восприятия виде. Дело
в том, что человек видит (воспринимает глазами) плоские картины (изображения).
Правда, два глаза создают некий стереоскопический эффект, намекающий на трёхмерность
рассматриваемого пространства. Однако изображение на сетчатке каждого из глаз –
плоское. Далее мозг человека уже обрабатывает эти плоские экраны, создавая в
воображении ощущение объёмности.
Эволюция человека ещё не достигла такого
уровня, когда он непосредственно мог бы увидеть третье измерение, хотя
отдельные люди, говорят, что они видят «сквозь стены». Мы можем допустить, что
это возможно, хотя научно подтверждённых данных, главное, объяснений физической
природы этого явления пока, насколько мне известно, не существует. Но ведь есть
приборы и системы, с помощью которых человек проникает в третье измерение:
рентгеноскопия, томография, ультразвуковая диагностика и т.д.
Можно сказать, что в определённый момент
(точке бифуркации) эволюция привела к разветвлению: человек стал изобретать, ТО
ЕСТЬ ДЕЛАТЬ ТО, ЧТО как мы природой не предусмотрено, ТО, ЧТО МОЖЕТ ДЕЛАТЬ
ТОЛЬКО ЧЕЛОВЕК.
То есть, обычного естественного
природного развития по законам дарвиновской эволюции оказалось недостаточно.
Необходимо было изобретать ПРЕДМЕТЫ, С ПОМОЩЬЮ КОТОРЫХ ЧЕЛОВЕК ИЗУЧАЕТ И
ИЗМЕНЯЕТ МИР и ЗНАКИ, С ПОМОЩЬЮ КОТОРЫХ ЧЕЛОВЕК ИЗМЕНЯЕТ СЕБЯ (Концепция В. С.
Выгодского, согласно которой интеллект, сознание, духовная культура людей
зависит на 99% от знаковой среды обитания и только на 1% – от предметной среды
обитания).
Началась эволюция, которая существенно
определяется ТВОРЧЕСТВОМ ЧЕЛОВЕКА. Хотя возможно, что природа может, например,
прислав крупный метеорит на Землю, практически, уничтожить (или отбросить назад)
ТВОРЧЕСКУЮ ЭВОЛЮЦИЮ, уничтожив ВСЕХ ЛЮДЕЙ. Ну что ж, тогда ПРИРОДЕ придётся
начать всё сначала.
Примечание 2.
В соответствии с Квантовой Энтропийной
Логикой Теодора ван Хоуэна для квантовых систем существует закон сохранения
информации. Однако, для макро систем существование такого закона трудно
предположить, хотя такие попытки предпринимаются.
Итак, мы можем констатировать, что за
прошедшие триста с лишним лет ДСК нашла широчайшее применение в науке, технике,
производстве, образовании. С помощью ДСК (этого знака) человек изменяет себя в
процессе познания.
Так, например, вместе с идеями
начертательной геометрии Гаспара Монжа (около начала ХIX века) ДСК легла в основу
создания языка науки, техники и производства. Речь идёт о ЯЗЫКЕ ЧЕРТЕЖЕЙ.
Вспомним, например, три вида: фасад,
план, профиль. Увидев эти три проекции, человек может представить в своём
воображении трёхмерный объект. Но воспринимает-то он глазами плоские объекты!
С изобретением этого нового языка
(чертежей) постепенно прекратилась утечка голов в области производства. Стало
возможным передавать чертежи, и по ним без участия рабочих, инженеров,
архитекторов и т.д. можно было изготовить необходимые технические объекты
(сооружения). Как известно, до этого времени, необходимо было приглашать
носителей информации, например, о строительных объектах. Вспомним, например,
многих архитекторов из-за границы, которых приглашали в Россию.
Конечно, если мы хотим воспользоваться
творческим потенциалом, утечка голов, если её не запретить, останется. Всё дело
в том, что мы не только не знаем, как протекают (осуществляются) творческие
процессы, мы не умеем адекватно записывать мысли, особенно в гуманитарных
областях. Известная письменность, назовём ей первой, обладает рядом недостатков,
которые приводят к значительным трудностям при попытке выразить мысли. Но об этом речь впереди.
Приступим к познанию МСКФ.
Федосеев
Р.Ю.
МНОГОМЕРНАЯ СИСТЕМА
КООРДИНАТ ФЕДОСЕЕВА
Краткая аннотация
МСКФ - Многомерная
Система Координат Федосеева - система координат, имеющая ячеистую (сотовую)
структуру, предназначенная для наглядного изображения на плоскости бумаги,
экране компьютера и др. или в трёхмерном пространстве зависимостей между
несколькими переменными.
Теоретически количество переменных может
быть выбрано от одной до бесконечности. Практически, количество переменных
ограничено размерами экрана (бумаги), разрешающей способностью нанесения и
считывания изображений или памятью и быстродействием компьютера.
Каждая переменная может принимать конечное
количество значений. Количество комбинаций значений переменных, всех
задействованных в данном изображении данной системы переменных, равно
произведению количеств значений каждой переменной и равно количеству ячеек
(сот).
Обычно ячейки имеют прямоугольную
(квадратную) форму. В ячейку (прямоугольник, квадрат и т.п.) можно занести
информацию о данной комбинации значений всех переменных.
Получающееся изображение системы координат
названо автором дешграммой. Дешграмму ещё можно назвать матрицей или просто
таблицей. Переменные на этой дешграмме имеют оси (прямые линии), на которые
нанесены все возможные значения этих переменных в виде отрезков прямых. Для каждого набора переменных и их
значений должна быть построена уникальная дешграмма, то есть своя система
координат.
Оси переменных расположены обычно по
сторонам параллелограмма, прямоугольника, ромба или квадрата (чаще всего
квадрата, но не обязательно). Квадрат имеет четыре стороны (оси), то есть,
достаточен для изображения системы координат для четырех переменных.
Если переменных пять или больше, то оси
изображаются параллельно сторонам квадрата (с внешней стороны). Можно сказать,
что наращивание переменных и осей для них производится по спирали. При этом
возможно “закручивание” спирали как по часовой, так и против часовой стрелке.
Пока принято “закручивать” по часовой стрелке.
Каждая ось
делится на количество отрезков, которое равно количеству значений переменных.
При этом можно начать отсчёт количества значений переменных с единицы, а можно
с нуля, полагая, что значение переменной равно нулю. В этом последнем случае
“автоматически” проектируется одна из позиционных систем счисления, в которой
может быть одно основание, если все переменные имеют одинаковое количество
значений, например, семь значений. А может быть спроектирована “новая” (в
смысле, не изучавшаяся и не применявшаяся на практике ранее) позиционная
система счисления, если хотя бы у одной из переменных, задействованных в данной
системе координат, количество возможных принимаемых значений не равно
количеству значений других переменных. Или же, вообще, у нескольких переменных
количества возможных принимаемых значений различны. При этом в ячейку,
соответствующую определённой комбинации значений всех переменных можно записать
число в десятичной или любой другой системе счисления, равное числу,
изображаемому в получившейся в процессе проектирования данной МСКФ системе
счисления.
Количество ячеек всегда равно количеству
возможных чисел, которые можно записать в проектируемой системе счисления.
В начале построения дешграммы (то есть
МСКФ) для заданного количества переменных, например, четырёх, берут
параллелограмм, например, квадрат, и нижнюю сторону отводят для первой переменной, левую сторону - для второй, верхнюю сторону
- для третьей, правую сторону - для четвёртой. А для изображения пятой, шестой,
седьмой, восьмой переменных строят
вокруг начального квадрата ещё одни квадрат и т.д.
Основной
“изюминкой” построения МСКФ является разбиение оси, на которую наносятся
отрезки, соответствующие значениям данной переменной, таким образом, что
учитывается разбиение оси предыдущей переменной, расположенной (оси,
расположенной) напротив “разбиваемой” оси. Так первая ось, соответствующая первой
переменной, разбивается на несколько отрезков (по количеству значений первой
переменной). И одновременно ось третьей переменной, расположенная на
противоположной стороне параллелограмма, также “разбивается” на такое же
количество отрезков. Вспомним, что у
любого параллелограмма (у прямоугольника, ромба, квадрата) противоположные
стороны параллельны. А когда дело доходит до “разбиения” на отрезки третьей
переменной (в соответствии с количеством её значений), то разбивается уже не
вся ось третьей переменной, а каждый отрезок этой оси, уже разбитый при
разбиении на отрезки оси первой переменной, расположенной напротив. Точно так
же поступают и при разбиении на отрезки других переменных. Таким образом,
получается дублирование отрезков, изображающих значения переменных, начиная с
третьей, и при поиске ячейки,
соответствующей заданному набору значений переменных учитывают только те
отрезки, которые находятся напротив отрезков, соответствующих заданным значениям
предыдущих переменных. Так, если для первой переменной задано значение “два”, а
для третьей переменной задано значение “три”, то на оси третьей переменной
выбирают отрезок, находящийся напротив отрезка со значение “два” для первой
переменной, и на нём уже выбирают отрезок со значением “три” для третьей
переменной.
МСКФ можно назвать также “Спиралевидной
Системой Координат” или “Периодической
Системой Координат”. Во всяком случае, она обладает свойствами спирали и
периодичности.
Кроме того, с ростом количества переменных
дешграмма начинает обладать свойствами фрактала. Фрагмент дешграммы при большом
увеличении выглядит так же, как и вся дешграмма в целом. При ещё большем
увеличении получаем ту же картину.
ДЕШГРАММНАЯ МАТРИЦА
или
МНОГОМЕРНАЯ
СИСТЕМА КООРДИНАТ
“...открытие простых символических обозначений, которые сами
приводят к манипуляциям по формальным правилам, явилось одним из путей, из
которых развилась мощь современной математики”.
Стефен Клини
“Я уверен, что плохая
голова, упражняясь в использовании вспомогательных средств (знаков), может
превзойти самую лучшую, подобно тому, как ребёнок может провести линию по
линейке лучше, чем самый искусный мастер от руки. Гениальные же умы, снабжённые
такими преимуществами, пошли бы несравненно дальше”.
Лейбниц
“История математики
показывает, что многие разделы этой науки стали успешно разрабатываться только после
того, как были введены удобные (эргономические) знаки, способствующие развитию
соответствующих рассуждений и построений”.
Паронджанов
Я предлагаю новый удобный “знак”,
“вспомогательное средство” для “рассуждений и построений” - ДЕШГРАММНУЮ МАТРИЦУ или, короче, ДЕШГРАММУ.
Дешграмма выполняется в виде таблицы, в
которую заносится информация, соответствующая набору значений ряда переменных.
При этом количество переменных может изменяться от одной до бесконечности, хотя
практически, показать на листе бумаге (или экране компьютера) можно только
конечное количество переменных.
Дешграмма - это не обычная таблица.
Дешграмма строится по особым правилам. Эти правила заключаются в следующем.
Далее смотри мою статью “ДЕШГРАММНАЯ
ТЕОРИЯ”, которую я здесь продолжаю.
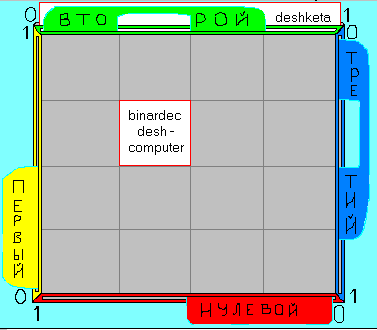
ДЕШГРАММНАЯ ТЕОРИЯ

МСКФ – Многомерная Система Координат Федосеева и дешкомпьютер, на
основе которых разрабатывается ДЕШИФРАТОРНАЯ ТЕХНОЛОГИЯ – это новая область
науки, техники, производства и применения дештоваров и дешуслуг, в частности
для образования.
Изобретатель Федосеев Р.Ю.
автор сотен запатентованных и используемых в народном хозяйстве разных стран
изобретений. Он является инициатором новых областей науки и техники:
ИНТЕЛЛЕКТОЛОГИИ, ТЕПЛОНИКИ, ЛАЗЕРОГРАФИИ,
ДЕШТЕХНОЛОГИИ.
Изобретения Федосеева в
течение сорока лет используются в различных отраслях промышленности разных
стран мира. Наиболее ценные из них вошли в учебники и служат не только в
народном хозяйстве, но и в системе  образования и подготовки
квалифицированных специалистов в области приборостроения и автоматики.
образования и подготовки
квалифицированных специалистов в области приборостроения и автоматики.
Федосеев Р.Ю. является
выдающимся
концептуальным изобретателем
России.
У Федосеева много
последователей и учеников, развивающих его концептуальные идеи.
Ученики и дети из подшефных
школ называют его «папой Робертом». Создан и успешно работает неформальный
Коллектив Разработчиков Дешифраторной технологии, который предлагает вниманию
школьников, родителей, педагогов и деловым людям Новые Общенаучные Базовые
Знания: теории, методологии, методики, конструкции, расчёты, чертежи, макеты и
другие материалы, которые представлены в серии брошюр «ДЕШИФРАТОРНАЯ
ТЕХНОЛОГИЯ»
В основе дешграммной теории лежит мое изобретение, которое я
называю ДЕШГРАММОЙ, а также МНОГОМЕРНАЯ СИСТЕМА КООРДИНАТ, которую называют
МНОГОМЕРНОЙ СИСТЕМОЙ КООРДИНАТ ФЕДОСЕЕВА (сокращённо – МСКФ), чтобы отличить от
всем известной декартовой системы координат.
ДЕШГРАММА - это особым образом организованная таблица (бланк),
которую можно изобразить на плоскости, а также сделать трёхмерной, то есть
изготовить в виде объёмной конструкции.
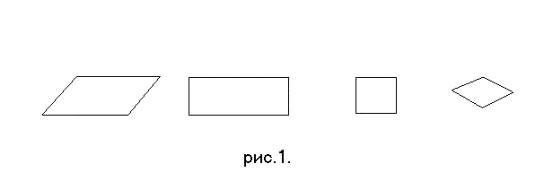
Изобразим на плоскости параллелограмм, в частности, прямоугольник,
или квадрат (см.
рис. 1.). Параллелограмм (прямоугольник, ромб, квадрат) имеет четыре
попарно параллельные стороны. Это четыре отрезка прямых линий, контактирующих
между собой концевыми точками. Между этими отрезками могут быть прямые углы (в
прямоугольнике и квадрате), а могут быть и острые и тупые углы (как в ромбе).
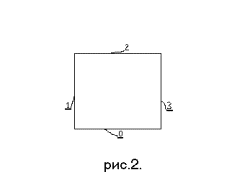
Обозначим числами 0, 1, 2, 3 эти отрезки прямых линий,
образующие параллелограмм, по порядку, начиная, например, с нижнего по чертежу
отрезка и по часовой стрелке (см.
рис. 2.).
Поле (часть плоскости, например, листа
бумаги), на котором изображен параллелограмм, заключенное внутри замкнутой ломаной
линии, состоящей из пронумерованных отрезков, назовем ячейкой. Эту одну ячейку
будем называть основной.
Договоримся размещать внутри ячейки какую-либо информацию в виде
знаков или рисунков.
Рассмотрим систему переменных (несколько переменных), каждая из
которых может принимать только одно значение. Из значений этих переменных мы
сможем составить всего одну комбинацию. При этом понятно, что количество
комбинаций значений каждой переменной или, попросту, количество значений каждой
переменной, мы приняли за единицу. При этом мы рассматриваем всю систему в
целом, то есть все переменные одновременно. При этом еще важно подчеркнуть, что
каково бы ни было количество таких переменных (имеющих только одно значение), мы получим всего одну комбинацию значений
всех этих переменных. Понятно, что если у переменной нет значений, то нет и
переменной, следовательно, минимальной количество значений переменной равно единице, а максимально
количество значений не будем ограничивать, но при конкретном рассмотрении
зафиксируем определенное количество значений.
При этом означенная выше ячейка адекватно представляет эту одну
комбинацию значений переменных (рис. 2.).
Далее, продолжим отрезок под номером "3" вниз на
величину, достаточную для фиксации нашим сознанием факта увеличения этого
отрезка, например, на величину 4 мм. (см. рис. 3.).
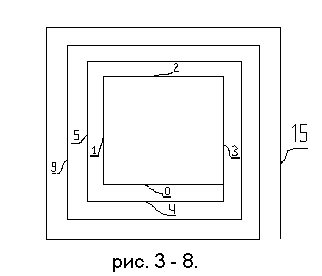
Далее,
проведем новую линию, параллельную отрезку под номером "0" и
величиной несколько большей, чем этот отрезок (например, на те же 4 мм. (см.
рис. 4.). Далее проведем новую линию, параллельную отрезку под
номером "1" и
величиной несколько большей этого отрезка... и т.д. по часовой стрелке. У нас получится
нечто, напоминающее ломаную спираль (см.
рис. 5, рис. 6, рис. 7., рис. 8.).
Продолжим обозначать числами новые отрезки по порядку по часовой
стрелке: 4, 5, 6, 7, 8, 9 и т.д.
Теперь представим себе, что одна из переменных может принимать
два значения. Тогда количество комбинаций значений всех переменных
(подчеркиваем: при любом количестве переменных) будет равно двум. А изобразить
это можно так, как это показано на
рис. 9.
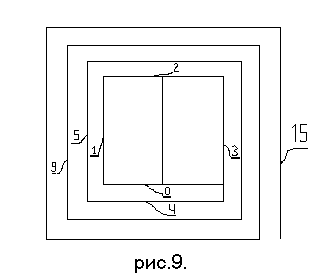
Мы просто делим,
например, "нулевой" отрезок
пополам и проводим линию внутри первоначальной ячейки. Получилось две ячейки,
каждую из которых можно поставить в соответствие с каждой из двух возможных
комбинаций всех значений переменных, сколько бы значений переменных у нас ни
было.
Для примера покажем, что можно присвоить два значения любой
другой переменной, например, переменной под номером "8" (см. рис.
10.).
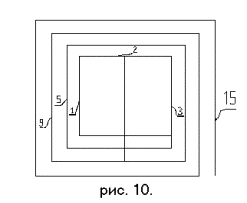
Другой пример см. на рис.
11. Два значения имеет переменная под номером "7".
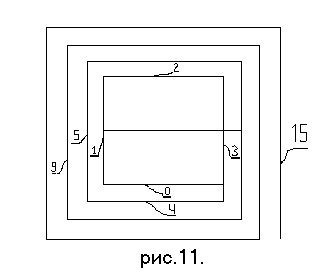
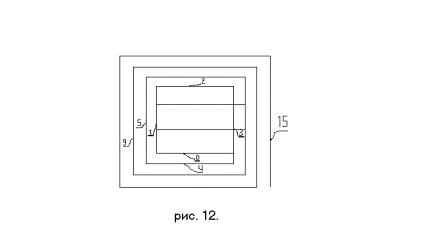
Если какой-нибудь одной переменной присвоить три, четыре, пять и
т. д. значений, то первоначальную ячейку мы разделим на соответствующее
количество частей, проведя соответствующие линии (см. рис. 12., на котором показана
ситуация с тремя значениями одной из переменных). При этом подчеркиваем, что
общее количество комбинаций всех значений всех переменных (сколько бы их не
было) будут равно количеству значений этой переменной.
Теперь мы можем представить ситуацию, когда несколько переменных
имеют не одно, а несколько значений.
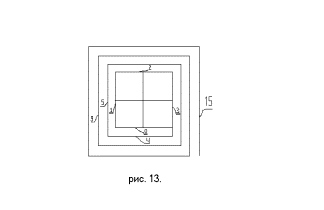
Например, переменная под номером "0" имеет два
значения и переменная под номером "1" имеет два значения (см. рис. 13.). Общее количество
комбинаций значений всех переменных будет равно четырем. Количество ячеек равно
количеству этих комбинаций.
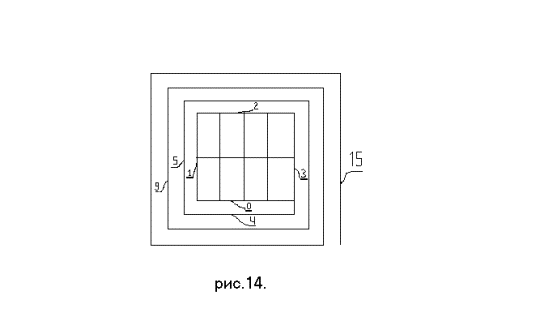
Если три переменных имеют по два значения, получим всего восемь комбинаций
значений переменных, им соответствуют восемь ячеек (см. рис. 14.).
В том случае, когда у какой либо
переменной "возникает" (мы присваиваем и т.п.) несколько значений, то
графически это показывается на поле
основной ячейки в зависимости от того, на сколько частей она уже разделена.
Например, вводя третью переменную с несколькими значениями по порядку номеров,
мы обнаружим, что основная ячейка уже разделена на две части, которые
соответствуют двум значениям переменной под
номером "0". В этом случае мы должны разделить каждую из
получившихся частей (ячеек) на количество частей, соответствующее количеству
значений третьей переменной. Это существенный момент.
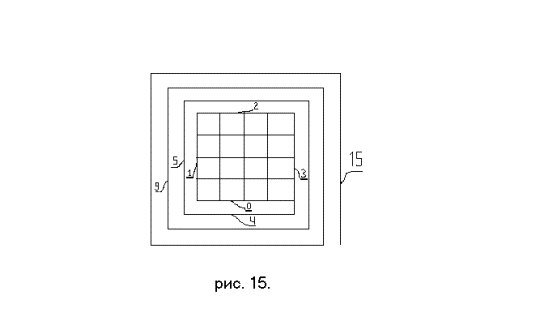
Если четыре переменных имеют по два значения, получив всего
шестнадцать комбинаций значений переменных, им соответствуют шестнадцать ячеек
(см. рис. 15.).
Если одна из переменных может принимать три значения, вторая два
значения, третья - четыре значения, четвертая - два значения, пятая - три
значения, шестая - ... и т. д., то чтобы узнать количество возможных комбинаций
значений всех переменных, надо перемножить количества значений каждой из
переменных.
Например:
|
№ перемен |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Всего |
|
Кол. знач. |
2 |
3 |
5 |
4 |
6 |
1 |
1 |
2 |
1440 |
|
Кол. знач |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
Кол. знач |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
256 |
|
Кол. знач |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
6561 |
|
Кол. знач |
5 |
1 |
1 |
3 |
7 |
9 |
2 |
3 |
5670 |
|
Кол. знач |
2 |
3 |
4 |
3 |
2 |
3 |
4 |
3 |
5184 |
|
Кол. знач |
13 |
24 |
32 |
12 |
1 |
23 |
1 |
5 |
13777920 |
|
Кол. знач |
123 |
3 |
4 |
3 |
2 |
3 |
4 |
3 |
318816 |
Таким образом, можно построить ДЕШГРАММУ
для отображения ВСЕХ комбинаций значений всех переменных заданной системы
переменных. При этом ни количество переменных, ни количество значений каждой
переменной ничем не ограничено. Можно теоретически рассматривать любые
значения. Но, конечно, из практических соображений, когда мы это все отображаем
не в компьютере, а на бумаге, то приходится вводить некоторые ограничения,
связанные с разрешающей способностью нашего зрения или удобствами работы с
большими бумажными листами и т.п. Но в компьютере ограничения существенно
сокращаются или, другими словами, компьютер с большой памятью и большим экраном
позволяет вводить миллионы переменных со многими значениями у каждой
переменной. Если память компьютера была бы неограниченной, то и количество
переменных и их значений было бы неограниченным. Для очень многих практических приложений современных
(2004 г.) возможностей компьютера вполне достаточно. Даже простые механические
дешкомпьютеры позволяют использовать дешграммы для создания мощных практически
полезных программ.
Построив дешграмму, для нескольких переменных, каждая из которых
имеет несколько значений (см. таблицу № 1), мы получаем некоторое количество ячеек
(параллелограммов), в которые мы можем записать некоторую информацию о данной
комбинации значений этой системы переменных.
Количество ячеек равно количеству комбинаций значений всех этих
переменных.
Каждой ячейке соответствует одна и только одна комбинация
переменных.
Каждой комбинации значений переменных соответствует одна и
только одна ячейка.
При этом, зная комбинацию значений переменных (зная конкретные значения каждой
переменной), можно легко, просто и быстро
найти уникальную соответствующую этой комбинации ячейку.
И наоборот, можно легко, быстро и просто определить каждое
значение каждой переменной, если задана ячейка.
Получилась своеобразная многомерная система координат.
Координаты каждой ячейки заданы значениями переменных (комбинацией значений
переменных).
Эту систему можно представить как модель устройства, выходной
сигнал которого - это значение, записанное в соответствующей
ячейке. Каждой комбинации входных сигналов соответствует одно и только одно
значение выходного сигнала, записанное в соответствующей ячейке.
Можно, например, зафиксировав значения всех переменных, кроме
одного, наглядно проследить зависимость выходного сигнала от одной из
переменных.
Ячейки можно называть
"экранами" или "ячейками памяти".
Используя принцип изометрии можно построить ОБЪЁМНУЮ ДЕШГРАММУ.
А, используя принципы начертательной геометрии и черчения можно построить три
вида и различные разрезы объёмной дешграммы.
Архитектура дешграммы является архитектурой компьютеров нового
класса (типа) - ДЕШКОМПЬЮТЕРОВ, а также
программ нового класса (типа), которые можно положить в основу принципиально
новых архитектур "баз данных"
и "баз знаний". Дешграмма является также основой построения
новых архитектур компьютерной памяти, которую можно назвать "ассоциативной
памятью".
На прилагаемых рисунках и фотографиях показаны различные
возможности использования предлагаемой МНОГОМЕРНОЙ СИСТЕМЫ КООРДИНАТ.
1.
Рисунок БИНАРДИКА
– первого двоичного четырёхразрядного персонального карманного дешкомпьютера,
который изобретён Федосеевым Р.Ю. в 1960 году.
2.
Рисунок
более сложного дешкомпьютера (одного из неограниченного множества возможных
и осуществимых реально, например, по методологии «РУССКОЕ ОРИГАМИ»).
3.
Фотографии
нескольких дешкомпьютеров, изготовленных по методологии «РУССКОЕ ОРИГАМИ».
Смотрите также брошюры
«БИНАРДИК
- РУССКИЙ КОМПЬЮТЕР».
Дешграмма также является основой визуальной многозначной логики.
С помощью дешграммы легко и наглядно представить логические соотношения
переменных.
Дешграмма может лечь в основу МОДЕЛИ ИНТЕЛЛЕКТА.
Продолжение следует на ВЕБ-узлах http://robfed.narod.ru и в других хранилищах: интернете, бумажной печати и др. ЧИТАЙТЕ статьи и книги по ДЕШИФРАТОРНОЙ
ТЕХНОЛОГИИ, РУССКОМУ ОРИГАМИ, ИНТЕЛЛЕКТУАЛЬНОМУ ШЕЙПИНГУ. Смотрите гипертекстовые
мультимедийные продукты на CD, DVD и на других
носителях. Можно получить также видео и аудио кассеты с учебным,
технологическим, рекламным и ознакомительным содержанием.
Получите
(в том числе, бесплатно) лицензии на производство ДЕШКОМПЬЮТЕРОВ, ДЕШПРОГРАММ,
КНИГ и т.д.
Приглашайте
членов КРД на презентации и консультации, на которых вы получите ноу-хау по
ДЕШТЕХНОЛОГИИ, которые невозможно все выложить в открытой печати, в связи с их
большим объёмом, тонкостями и
сложностями их публичного отображения.
Это реальный БИНАРДИК (конструкция
Семёнова А.Н.) - практически
проверенный и применяемый школьниками с первого по третий класс по методике
Т.В. Кириной «Первые шаги в образовании».

Рисунок
первого двоичного четырёхразрадного персонального карманного дешкомпьютера,
изобретённого Федосеевым Робертом Юрьевичем в 1960 году.

Фотографии нескольких
дешкомпьютеров, изготовленных по методологии «ИНФООРИГАМИ» («РУССКОЕ ОРИГАМИ»).

Рисунок
более сложного дешкомпьютера (одного из неограниченного множества возможных и
осуществимых реально, например, по методологии «РУССКОЕ ОРИГАМИ»).

Вот так реализуется на
практике идея МНОГОМЕРНОЙ СИСТЕМЫ КООРДИНАТ ФЕДОСЕЕВА.
И это ещё цветочки, а ягодки
вы можете получить у КРДТ –
Коллектива Разработчиков
Дешифраторной Технологии
Теперь продолжим разговор о ДЕШГРАММЕ, как новом ЗНАКЕ, с
помощью которого мы можем наглядно представить многомерную и многозначную
систему координат.
Дешграмма – это таблица, состоящая из ячеек. Можно говорить
также о столбцах и строках таких ячеек.
Каждая ячейка соответствует одной единственной комбинации
значений всех используемых в данной дешграмме переменных.
Вот несколько примеров дешграмм. Дешграммы обозначаются
числами, соответствующими количеству значений каждой переменной. Сначала
указывается число, соответствующее количеству значений первой переменной
(обычно она соотнесена с нижней стороной параллелограмма, но возможны
варианты). Между этими числами ставится
знак умножения (любой, например, точка или крестик в виде буквы “х”) и т.д.
Далее ставиться знак равенства. Далее
результат умножения этих чисел.
Дешграмма 2 х 2 х 2 х 2 х 2
х 2 = 64
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
Х |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
0 |
Отметим, что на показанной дешграмме строчки и столбцы, в
которых записаны числа от 1 до 8 в дешграмму не входят. Они нужны для
пояснений. Это номера столбцов и строк.
Итак, в нашей дешграмме восемь столбцов и восемь строк.
Как следует из формулы дешграммы (2 х 2 х 2 х 2 х 2 х 2 = 64),
имеется шесть переменных, каждая из которых может принимать одно из двух
значений. Всего 64 комбинации значений переменных.
Первое значение первой переменной означает, что мы выбираем
столбцы с номерами 5,6,7,8.
Второе значение первой переменной означает, что мы выбираем
столбцы с номерами 1,2,3,4.
Первое значение второй переменной означает, что мы выбираем
строки с номерами 5,6,7,8.
Второе значение второй переменной означает, что мы выбираем
строки с номерами 1,2,3,4.
Первое значение третьей переменной означает, что мы выбираем
столбцы с номерами 1,2,5,6.
Второе значение третьей переменной означает, что мы выбираем
столбцы с номерами 3,4,7,8.
Первое значение четвёртой переменной означает, что мы выбираем
строки с номерами 1,2,5,6
Второе значение четвёртой переменной означает, что мы
выбираем строки с номерами 3,4,7,8.
Первое значение пятой переменной
означает, что мы выбираем столбцы с номерами 1,3,5,7.
Второе значение пятой переменной означает, что мы выбираем
столбцы с номерами 2,4,6,8.
Первое значение шестой
переменной означает, что мы выбираем столбцы с номерами 1,3,5,7.
Второе значение пятой переменной означает, что мы выбираем
столбцы с номерами 2,4,6,8.
Таково принятое нами только что соглашение о выборе столбцов и
строк матрицы при определённых значениях переменных. Это соглашение могло бы
быть и иным. Например, можно договориться, что первое значение всех переменных
присваивается всем “правым” столбцам, второе значение всем “левым” столбцам и
далее по часовой стрелке (или против часовой стрелки). Мы подчёркиваем, что
такое соглашение должно быть оговорено. Иногда удобно принять одно и то же
соглашение для всевозможных дешграммных матриц (стандарт).
Предположим, у нас имеется набор шести переменных, каждая из
которых имеет первое значение.
Эта комбинация значений переменных однозначно соответствует
ячейке матрицы, лежащей одновременно на пятом столбце и пятой строке (ячейка
помечена крестиком).
На первый взгляд кажется, что поиск нужной ячейки по
координатам не так прост, как хотелось бы. Но практика показывает, что это дело
привычки, наработки навыка. Имеется также возможность введения в дешграмму
дополнительных обозначений. Например, цветом столбцов и строк, соответствующих
разным переменным, а также разным значениям переменных. Можно применить
дополнительные обозначения “вокруг” дешграммы. Можно также использовать
специальное приспособления, которое я назвал “дешкомпьютером”.
Это устройство состоит из “клавиш”, количество которых равно
количеству переменных. Эти клавиши устанавливают в положения, соответствующие
значению данной переменной (см. рисунки и фотографии таких дешкомпьютеров). Эти клавиши показывают, какие из столбцов
выбраны или перекрыты (т.е. исключены из рассмотрения).
Имеется также возможность выполнить дешкомпьютер с клавишами в
виде пластин, перекрывающих определённые части столбцов и строк (см. фото и
рисунки.). В этом случае остаётся одна и только одна «открытая» ячейка, с
которой можно считать информацию. А координаты, то есть значения всех
переменных можно “считывать” по положению клавиш. Разумеется, что координаты
(то есть значения каждой переменной) можно устанавливать этими клавишами.
Таким образом, вводится новая многомерная система координат, с
помощью которой можно наглядно проследить все взаимозависимости многих
переменных на плоскости, если каждой переменной присваиваются конечные
значения. Если же значения переменных аналоговые (непрерывные), то есть могут
принимать любые значения на отрезке, то можно эти переменные дискретизировать с
любой наперёд заданной точностью. Естественно, для этого требуется либо значительные
плоскости бумажного носителя, либо компьютерная технология, позволяющая
выводить на экран отдельные участки матрицы “почти” бесконечной величины (это зависит от характеристик компьютера, в
основном, от памяти и быстродействия).
Рассмотрим другие примеры
дешграммных матриц (дешграмм) с другими наборами переменных и их значений.
Дешграмма 2 х 3 х 4 х 5.=
120
Дешграмма 2 х 3 х 2 х
3.= 36
Дешграмма 2 х 3 х 5 х 5.=
150
Дешграмма 2 х 3 х 2 х 2
= 24
Дешграмма 2 х 3 х 4 х 5.х 2
х 3 = 720
Таким образом, мы получили удобную форму представления
зависимостей многих переменных на плоскости. Что касается трёхмерного
пространства, то легко представить объемную трёхмерную дешграмму, с помощью которой можно поставить в
соответствие объёмную же ячейку внутри параллелепипеда, выделив на каждой из
трёх перпендикулярных плоскостей ячейку соответствующую заданным значениям
заданных переменных.
Продолжение следует.
Будут рассмотрены различные варианты
дешграмм и их применение в науке и технике. В частности, для моделирования
искусственного интеллекта (ассоциативной памяти и др.), для построения
дешграммных архитектур компьютеров и компьютерных программ и др.
МСКФ - МНОГОМЕРНАЯ СИСТЕМА
КООРДИНАТ ФЕДОСЕЕВА
тезисы
1. Подобно тому, как отец современного менеджмента
Питер Дракер утверждает, что “знания являются главным экономическим ресурсом”,
я считаю знания - самым главным оружием.
Действительно, очевидно, что даже слабенькая в экономике в обычном плане
страна, например, Россия, благодаря знаниям, владеет атомным оружием и
выступает, подчас, на равных с экономическим монстром - США. Бывший министр
обороны США Пери заявил недавно, что “через пять лет мощь страны будет
определяться не ракетами и бомбами, а программистами”.
2. Но, спрашивается, кто мешает использовать большой
потенциал знаний, накопленный в России, чтобы вырасти экономически?
И есть
ли этот потенциал?
3. Я предлагаю добавку в этот потенциал -
Многомерную Систему Координат Федосеева.
4. Рассмотрим задачу, которую я решаю с помощью
МСКФ.
Даны
несколько переменных, например, пять, каждая из которых задана набором значений
в определённом диапазоне.
С
помощью методики (алгоритмов и правил) я строю на плоскости (листе бумаги или экране
компьютера) изображение этой системы координат - дешграмму, на которой можно
будет:
- показать
одну и только одну точку (с окрестностями), однозначно соответствующую
заданному набору значений переменных, то есть, по заданному набору значений
переменных найти точку с окрестностями на листе бумаги;
- указав точку на этой дешграмме, то есть на
изображении заданной системы координат, можно найти все координаты, то есть
значения всех входящих в заданную систему переменных, однозначно соответствующие
указанной точке.
Это
достигается благодаря изобретённому
мной особому приёму построения дешграммы.
5 . Перечислим области применения МСКФ:
5.1.
Прежде всего, это создание наглядных логических описаний (моделей) предметных
областей, описываемых многими многозначными переменными. Для создания
логического исчисления дешграмм.
5.2.
Создание новых архитектурных схем компьютеров.
5.3.
Создание новых архитектурных схем компьютерных программ.
5.4.
Создание новых интерфейсов для компьютерных программ.
5.5. Для
реализации манипуляторов для компьютеров.
5.6. Для
реализации ИНТЕРФЕЙСА.
5.7. Для
конструирования компьютеров нового класса -
ДЕШКОМПЬЮТЕРОВ.
.5.8. Для
разработки дешкомпьютерных программ (дешпрограмм).
5.9. Для
создания механизмов нового класса, так называемых ИНФОРМАЦИОННЫХ МЕХАНИЗМОВ,
которые можно в различных областях, например, для создания приборов, мебели,
замков, игрушек, тира, фотоаппаратов, рекламных стендов и многих других
устройств.
5.10. Для
создания учебных пособий табличного типа.
5.11. Для
создания электронных и других микросхем с дешграммной топологией.
5.12. Для
создания новых суперязыков диаграммного вида (диосцены). Дешграммная
письменность.
5.13. Для
создания новых языков программирования для электронных компьютеров.
5.14. Для
создания дешвордов и других учебных пособий в области словесности.
16. Выводы
6.1.
Создано новое знание - МСКФ.
6.2. МСКФ -
проста, понятна и красива. Следовательно, будет востребована. И она уже
востребована для образования. Построены первые образцы дешкомпьютеров и
дешпрограмм, которые уже несколько лет с успехом применяются в семьях, детских
садах и школах.
6.3. Надо
широко оповестить общественность. МСКФ включить во все соответствующие
учебники: по математике, физике, химии, логике, информатике и всем другим.
6..4.
Предложить программистам и компьютерным специалистам воспользоваться МСКФ для
создания как обычных компьютерных программ, так и дешпрограмм.
6.5. Предложить
изобретателям, конструкторам, фирмам и др. использовать МСКФ для создания новых
полезных устройств и, в первую очередь, дешкомпьютерных устройств для оснащения
детей и взрослых.
6.6.
Начать дешкомпьютеризацию России, чтобы догнать и перегнать другие страны в
области информатизации, так как отставание в этой области грозит исчезновением
России.
Уточним название новой
письменности.
Новая письменность – вторая
письменность – многомерная письменность – дешграммная письменность – нелинейная
письменность… Термины ещё не устоялись. С нашей точки зрения наиболее
приемлемый термин – дешграммная письменность (потому что она основана на МСКФ –
Многомерной Системе Координат Федосеева, дешграмма – это изображение заданной
МСКФ на поверхности экрана). В дешграммной письменности мысли структурируются в
виде дешграммы в виде текстов, формул и чертежей (рисунков). Дешграмма – это
гипертекстовая среда.
$3.
Термин:
ДЕШИФРАТОРНАЯ ТЕХНОЛОГИЯ
3.1.
3.1.
Перевод термина
на англ.
THE DECODING TECHNOLOGY
3.2.
3.2.
Толкование.
Дешифраторная технология – это обширная область человеческой
деятельности, в которой применяются открытия и изобретения, связанные, в первую
очередь с МСКФ – Многомерной Системой Координат Федосеева.
К дешифраторной технологии
относятся:
·
· Теории, например,
ДЕШГРАММНАЯ ТЕОРИЯ, занимающаяся алгоритмами построения разнообразных систем
счисления и разнообразных систем координат.
·
· Изобретения, например,
ДЕШКОМПЬЮТЕР (изобретена новая архитектура компьютера, обеспечивающая ряд
преимуществ, например, по быстродействию и простоте реализации) и другие
ДЕШТОВАРЫ И ДЕШУСЛУГИ.
·
· Новые методологии и методики
программирования для компьютеров, например, ДЕШПРОГРАММИРОВАНИЕ (на
естественном, родном языке, а не на специальных «птичьих» языках).
·
· Новые методологии для
образования, например, РУССКОЕ ОРИГАМИ (другие альтернативные названия:
ИНФОРМАЦИОННОЕ ОРИГАМИ, ДЕШОРИГАМИ). РО – это методология для развития
творческих способностей детей с раннего возраста.
·
· Новые методологии для
интеллектуального развития взрослых, например, ИНТЕЛЛЕКТУАЛЬНЫЙ ШЕЙПИНГ –
методология ВУВЭРС – Восстановление Утрачиваемых (с годами) Возможностей Эффективного
Развития Способностей (по Федосееву Р.Ю.). Интеллектуальный шейпинг основан на
идеях новой области науки об интеллекте, которую её основатель – Федосеев
Роберт Юрьевич – назвал ИНТЕЛЛЕКТОЛОГИЕЙ.
·
· Новые области создания машин
и механизмов, так называемые «ИНФОРМАЦИОННЫЕ МЕХАНИЗМЫ».
·
· Новые области игр и
развлечений, например, ДЕШВОРД, ДЕШКИ и другие дешигры.
·
· Новые игрушки на основе
дешкомпьютеров.
·
· Новые товары бытового
назначения, например, мебель, замки, архитектурные сооружения, интерьеры жилых
и офисных помещений и т.д.
·
· Новые виды рекламы.
·
· Новые виды искусства,
например, ДешАрт.
·
· И ещё много и многое другое,
о чём можно узнать из системы сайтов в интернете:
$4.
Термин:
МСКФ – Многомерная Система Координат Федосеева. Изобретена
Федосеевым Робертом Юрьевичем в 1960 году вместе с первым дешкомпьютером
БИНАРДИКОМ – двоичным четырёхразрядным персональным карманным.
4.1.
Перевод термина
на англ.
FPCS
– THE POLI-DIMENSIONAL COORDINATES SYSTEM
4.2.
4.2.
Толкование.
Это изобретение можно назвать
«следующим шагом после Декарта». Дело в том, что МСКФ позволяет наглядно
показать на плоскости (листе бумаги или экране компьютера) взаимозависимости не
только двух, но и любого конечного множества многозначных переменных.
Алгоритмы построения конкретных МСКФ изучаются и предлагаются в
Дешграммной теории того же автора.
МСКФ
является основой изобретения дешкомпьютера (компьютера с дешграммной
архитектурой.
Основным
«козырным» термином МСКФ и Дешграммной теории является ДЕШГРАММА – это и есть изображение конкретной МСКФ на
плоскости. Возможны, однако, построения МСКФ в трёхмерном пространстве, но это
особая область, которая пока засекречена.
Дешграмма
– это новый знак, освоить который и пользоваться им может даже ребёнок.
Дешграмма предлагается как основа для новой ДЕШГРАММНОЙ ПИСЬМЕННОСТИ,
состоящей в том, что запись слов, формул и рисунков на плоскости структурируется именно в форме дешграммы.
Тогда возникают следующие преимущества: лучшее понимание смыслов передаваемых
письменно, убыстрение процесса восприятия и понимания письменного послания и
др.
МСКФ является основой ДЕШИФРАТОРНОЙ ТЕХНОЛОГИИ в целом, а также её
различных частей: от дешкомпьютеров и дешпрограммирования, до дештоваров и
дешуслуг.
В заключении привожу небольшой панигирик изобретателям
Человек изобретательный
спасёт мир. Дайте детям дешкомпьютер
с первых месяцев их жизни, и они не будут “трясти” всё и вся, а научаться
думать и изобретать, из каждого из них получится “человек
изобретательный”. (ЧЕЛОВЕК: Энциклопедический словарь. - М.: Гардарики, 1999. - 520 с.):
“ЧЕЛОВЕК
ИЗОБРЕТАТЕЛЬНЫЙ - человек, занимающийся инновационной деятельностью.
Современное состояние человечества представляет собой результат инновационной
изобретательской деятельности творческого человека на протяжении всей истории
общества. Консультант-редактор энциклопедии “Изобретения, которые изменили
мир” Г.Р. Тэйлор во вступительной
статье “Корни изобретения” пишет, что именно в умении, возможности изобретать
состоит глубочайшее отличие в образе жизни человека от поведения и
жизнедеятельности животных. Из всех десятков миллиардов человек (примерно 80
млрд.) живших и живущих ныне, только несколько тысяч были творческими гениями,
способными изобрести нечто новое и полезное. Их вдохновенная изобретательская
деятельность обусловила изменение численности и распределение населения нашей
планеты, внесла величайшие перемены в локализацию политической власти, создала
новые классовые системы, трансформировала воспитание и образование и т.п. “Кто
эти изобретатели? Какие мотивы двигали ими? Что придавало им смелость? Как они
могли сделать то, что не смогли другие? Эти вопросы представляют собой больше,
чем философский интерес, ибо связаны практически с экзистенцией человечества
(Тейлор). Именно в
результате изобретательской деятельности человека с самого рождения общества
появилась техника, а затем и наука”.
УНИВЕРСИТЕТ ФЕДОСЕЕВА http://robfed.narod.ru
ЧТО ТАКОЕ
ПИСЬМЕННОСТЬ И
ДЛЯ ЧЕГО НУЖНА
ДЕШГРАММНАЯ ПИСЬМЕННОСТЬ
Письменность настолько популярное и привычное понятие, что, казалось бы, не подлежит обсуждению.
Считается, что письменность родилась в виде клинописи на глиняных
табличках у шумеров пять или шесть тысяч лет назад. Её развитие за тысячелетия
привело к созданию наиболее доступного и экономного способа записи речи с
помощью звуков, то есть к алфавитному письму.
Древнегреческий алфавит был создан приблизительно три тысячи лет назад.
Алфавит
русских букв в почти современным виде был предложен Кириллом и Мефодием всего
каких-нибудь тысячу лет назад.
Алфавитное книгопечатание (с литерным набором текстов) осуществил в
пятнадцатом веке Гуттенберг.
Изобретение письменности в том виде, в котором мы её знаем, явилось
величайшим достижением человечества, однако опыт её использования показал, что
она обладает рядом существенных недостатков.
Прежде
всего, алфавитное письмо есть ни что иное, как запись звуков с помощью знаков.
Знаки записываются линейно (одномерно). Что происходит? Сначала мы пытаемся выразить
мысли через звуки с помощью слов. Затем мы записываем звуки с помощью знаков.
А нельзя
ли сразу непосредственно перейти от мысли к её изображению, минуя стадию
превращения мысли в слова и звуки?
Такие
попытки человечество делает с давних пор. Возьмём, к примеру, иероглифический
способ записи мыслей, в котором формируется знак, не обязательно осмысливаемый
через звуки. Иероглиф обозначает значительную часть мысли, которую не
обязательно проговаривать словами, то есть озвучивать. Однако освоение
иероглифического письма представляется трудной задачей для большинства людей,
так как требует запоминания огромного массива знаковой информации. Кроме того,
усложнение иероглифов для передачи более сложных мыслей влечет за собой
неимоверные дальнейшие затруднения дешифровки полученных текстов.
Примечание
1.
Запись мыслей можно рассматривать как процесс шифрования (или кодирования), а чтение записи – как процесс дешифровки (декодирования). Специалисты договорились, что термины «кодирование» и «декодирование» надо применять в теории и практике связи (передачи информации), а термины «шифрование» и «дешифрование» – в криптографии. Мы считаем, что при рассмотрении различных принципов письменности применение обоих видов терминов правомерно, так как знаковое, иероглифическое, клинописное и др. письмо применяются, как для того чтобы как можно точнее передать мысли, так и для того, чтобы как можно надёжнее скрыть их.
Может быть, для кого-то будет неожиданным моё предложение рассматривать изобразительное искусство (живопись, графику, скульптуру и т.п.) как письменность (различные её виды).
«Итальянский искусствовед Адольфо Вентури так писал о рисунках Леонардо Да Винчи: «Рисунок Леонардо подобен букве, слову, фразе. Проводя линию карандашом, углём или пером, художник говорит. Его письмо следует за ходом мысли, выявляет взгляд мастера на природу вещей».
В своих работах Леонардо тщательно прорабатывал каждую деталь (будь то цветок или травинка), добиваясь наибольшей выразительности. Об этом напряжённом творческом поиске мы имеем представление, благодаря дошедшим до нас многочисленным зарисовкам и штудиям великого художника. Каждая из них – бесценное свидетельство образа мысли Леонардо». (Это цитата из сборника «Художественная галерея». Полное собрание работ всемирно известных художников. Часть 7. Да Винчи, стр. 26).
Конечно, и нотная запись является письменностью. Но хороший музыкант и так слышит звуки, глядя на запись, а остальным, которых большинство, требуется озвучивание, но с помощью музыкальных инструментов или голоса.
Итак, определим письменность как попытку записать мысли на поверхности (листе бумаги, экране компьютера, холсте и т.п.). И не обязательно мысли кодировать или шифровать словами или нотами, то есть, озвучивать «про себя» или вслух.
Моя дешграммная письменность – это новый вид структурирования информации о мыслях и изображение её на поверхности бумаги или экране в виде дешграммы с применением рисунков, нот, математических, химических и других видов знаков, а также и обычного алфавитного или иероглифического письма. Дешграммная письменность – это попытка наиболее полно и точно записать, сохранить, передать, проанализировать именно мысли, это попытка устранить или снизить ограничения обычной письменность для записи звуков. Это попытка записи мыслей, а не звуков.
Дешграмма представляет собой особого рода матрицу, называемую МСКФ (Многомерной Системой Координат Федосеева), с помощью которой можно решить задачу о нахождении точки по координатам, либо обратную – нахождение координат заданной точки. Как известно, такую же задачу можно решить с помощью Декартовой Системы Координат (ДСК), но только для двух переменных (для трёх – в изометрии). МСКФ решает эту задачу для любого количества координат (заданных переменных).
Предположим, что задана предметная область, состоящая из четырёх
двухзначных переменных. Это – четырёхмерная МСКФ. Дешграмма для неё выглядит
так, как показано на рисунке. Алгоритмы построения дешграмм рассматриваются
в «Дешграммной Теории Федосеева», http://robfed.narod.ru (Этот сайт в конце 2004
года будет перенесён на адрес: http://fedoseev.info).
Мысль
можно определить как процесс создания в сознании человека модели предметной
области, состоящей из многих многозначных переменных. Мысль дискретна (то есть
состоит из взаимосвязанных переменных, принимающих дискретные значения). Одна
переменная может принимать три значения, которые мы учитываем, другая – пять,
третья – восемь, четвёртая – тринадцать и т.д.
Поскольку, переменные в модели предметной области взаимосвязаны
(взаимодействуют, а иначе, какой смысл включать в предметную область переменную,
которая никак не влияет на процесс мышления?), постольку, необходимо
рассмотреть «срезы» (состояния) динамической мысли при всех возможных
комбинациях значений этих переменных. При определённых сочетаниях значений
каждой переменной в рассматриваемой предметной области мы имеем в сознании некий
вывод, некое мнение, некое состояние, возможно, образ и т.п. В дешграмме есть место, в которое этот вывод
мы можем поместить. Это место называется «экраном» или «ячейкой памяти». Этот
экран имеет адрес (набор координат), который состоит из совокупности конкретных
выбранных значений каждой переменной, входящей в рассматриваемую предметную
область. То есть для каждой комбинации значений всех переменных данной
предметной области имеется свой экран с определённым адресом, равнозначным
набору значений всех переменных в заданной комбинации.
Поскольку, дешграмма представляет собой прямоугольную обычно плоскую
двумерную поверхность, которую можно одномоментно (симультанно) охватить
взглядом, постольку, все рецепторы зрительного органа человека участвуют в процессе
восприятия.
Известно, что обработка информации, поступающей через глаза, начинается
нейронными сетями, соединёнными с рецепторами («палочками» и «колбочками»).
Можно сказать, что «глаза – это вынесенный мозг».
Известно
также, что при чтении одномерной записи обычной письменности необходимо
концентрировать изображение на «желтом пятне» глаза (сукцессивное восприятие).
При этом остальные рецепторы, а, следовательно, и нейронные сети, то есть, этот
«вынесенные мозги» отключаются. Кроме того, восприятие букв происходит
последовательно, а не одномоментно.
Из этих
соображений можно сделать вывод о преимуществах дешграммной письменности,
которая нелинейна, позволяет одномоментно окинуть картину различных состояний
мысли (при различных комбинациях значений переменных), позволяет анализировать
предметную область во всей полноте, не пропуская различных возможностей. То
есть мысль можно выразить не только и столько словами, а в значительной мере
структурой, состоящий из различных комбинаций возможных оттенков мысли.
Конечно,
полное осмысление дешграммной письменности и её преимуществ ещё впереди, но
имеющийся опыт её применения уже многообещающь.
Автор концепции дешграммной письменности Федосеев Роберт Юрьевич
http://adresrobert.narod.ru http://fotorobert.narod.ru E-mail:robertfedoseev@nm.ru
Приглашаем
всех любознательных и образованных граждан, «считающих своё образование
незаконченным» (К. Симонов), на ознакомительный семинар «ДЕШГРАММНАЯ
ПИСЬМЕННОСТЬ ФЕДОСЕЕВА И ЕЁ
ПРИМЕНЕНИЕ».
Запись на семинар по телефонам: 269 51 52 и 919 44 19
E-mail:
robertfedoseev@nm.ru
УНИВЕРСИТЕТ ФЕДОСЕЕВА
Ознакомительный трёхчасовой семинар
«ДПФ – ДЕШГРАММНАЯ
ПИСЬМЕННОСТЬ ФЕДОСЕЕВА или
как записывать мысли с
помощью дешграммной письменности»
Специалист попадает в такие цели, в которые попадать он обучен и привык.
Далее
цитируем Шопенгауэра:
«Талант попадает в цели, в которые
специалисты и другие лица попасть не могут».
«Гений попадает
в цели, которые никто не видит».
Если говорить о целях участников
семинара, то в первую очередь нужно иметь в виду Новые Базовые Знания. «Базовыми я называю такие знания, которые
нельзя упростить без искажения смысла» (Федосеев). Семинар посвящен освоению
этих знаний.
Новые
Базовые знания, которые можно получить на семинаре – это:
1.
МСКФ
– Многомерная Система Координат Федосеева. Дешграммы и алгоритм их построения.
2.
Дешкомпьютеры.
3.
Дешпрограммирование
на естественном языке.
Дешграммная письменность для записи мыслей, а не звуков, основана на
этих базовых знаниях.
Эти базовые знания пока освоены лишь ограниченным количеством людей, поэтому их можно считать эксклюзивными. Эта информация новая и малоизвестная. Уместно вспомнить по этому поводу слова Черчилля: «Кто владеет информацией, тот владеет миром».
Освоение
этих знаний даёт следующие преимущества:
1.
Формирует
развитый аналитический механизм. «Никому и ни при каких обстоятельствах нельзя
объяснить больше того, чем он может освоить с помощью своего аналитического
механизма» (Игорь Серов). Другими словами улучшаются мыслительные способности.
2.
Умение
записывать и читать мысли на «языке дешграмм». Это равносильно знанию ещё
одного символьного языка, наподобие нотной грамоты или химических обозначений.
3.
Умение
пользоваться дешкомпьютером (обучение, развлечения, тестирование, визуальная
коммуникация и др.).
4.
Возможность
использования полученных знаний в обычной работе, бизнесе, изобретательстве,
научной деятельности.
Дешобразование можно продолжить, например, став участником или
сотрудником Университета Федосеева (с условиями можно ознакомиться на сайте http://robfed.narod.ru ).
Можно
будет также учиться в «Школе Дешграммной Письменности Федосеева» (Проект школы
разрабатывается). При этом можно будет получить следующие специальности: дешизобретатель, дешконструктор,
дешпрограммист, дешрекламист, дешпреподаватель, дешжурналист, дештеоретик, дешбизнесмен,
дешпродавец и др.
Созидается
новая отрасль науки, техники, производства и применения – ДЕШИФРАТОРНАЯ
ТЕХНОЛОГИЯ (кратко – ДЕШТЕХНОЛОГИЯ). Множество изобретений дештоваров и
дешуслуг предназначены для нового рынка – ДЕШРЫНКА. Это не занятая ниша на
рынке ИКТ (Информационно-Коммуникационных Технологий). Эта ниша относится к
товаром, стоимость которых, в основном, находится в пределах от одного ста долларов. Кроме того, область
применения этих товаров относится, в основном, к инструментам для обучения
детей и взрослых.
Кроме
того, такие товары, как дешмебель, дешзамки, дешархитектурные сооружения могут
продаваться на других соответствующих своему назначению рынках.
Возникает также новый вид искусства – ДЕШАРТ.
Многообразие
и широта применения новых базовых знаний может стать одной из причин
необходимости и полезности их освоения.
Мы
надеемся, что участники нашего семинара достойно оценят полученные на семинаре
знания и с пользой начнут их применять.
До начала
семинара Вы можете обратиться с вопросами по адресу: robertfedoseev@nm.ru
Запись на семинар по телефонам: 269 51 52 и 919 44 19
Место и время проведения семинара будут сообщены
дополнительно.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
Приведённых данных о книгах достаточно, чтобы их найти
через интернет магазины, например, «OZON».
- «Как улучшить работу ума» В. Д. Паронджанов.
- «Загадка капитала» Эрнандо де Сото.
- «Представьте себе» Петерсон (?).
- «Венчурный капитал» Кeтрин Кeмбэл (?).
- «Общество мечты» Рольф (?) Йенсен.
- «Бизнес в стиле фанк» Стокгольмская Школа Экономики.
- «Караоке капитализм» Стокгольмская Школа Экономики.
- «Революция в обучении» Гордон Драйден и Джаннетт Вос.
- «Нетократия» (?).
- «NEXT. Будущее уже началось. Как интернет изменил бизнес и мир» Майкл Льюис.
- «Интеллектуальные игры» Никитин Б. П.
- «Дешграммная письменность» Федосеев Р. Ю.
- «Творческое общество» Федосеев Р. Ю.
- «Настройся на гениальность» Федосеев Р. Ю.
- «Русское оригами» Федосеев Р. Ю.
- «Интеллектуальный шейпинг» Федосеев Р. Ю.
- «Дешифраторная технология» Федосеев Р. Ю.
- Сайты в интернете: http://robfed.narod.ru http://sisrobert.narod.ru
http://svakarobert.narod.ru http://35736.copi.ru
http://adresrobert.narod.ru http://graf-montekristo.narod.ru
http://rufproekt.narod.ru http://crsoc001.narod.ru (2,3 и т.д.).
Рассылки: 1. «Новости Университета Федосеева»; 2. «Новая письменность» и др.
- «Дорога в будущее» Билл Гейтс.
- «Бизнес со скоростью мысли» Билл Гейтс.
- Все последние книги Питера Друкера и Ф. Котлера.
- Предложите что-то новое и полезное для изучения! Добавьте!!!
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
e-mail:
robertfedoseev@nm.ru
См. также:
пока на сайте – http://robfed.narod.ru скоро на
сайте – http://fedoseev.info
http://trillioner.narod.ru http://ro.agava.ru http://crsoc.narod.ru
… crsos001…crsoc002…
http://adresrobert.narod.ru http://fotorobert.narod.ru http://35736.copi.ru
понедельник, 8 ноября
2004 г.
Ó Федосеев Р.Ю. Все права защищены патентами, публикациями и
другими способами.